1. Method of Selection
Many parameters are involved in the selection of an accumulator:
1). Minimum working pressure P1 and maximum pressure P2, the value of P2 must be lower or equal to the maximum authorized working pressure of the accumulator to be chosen for safety reasons.
2). Volume of liquid to be stored or utilized.
3). Method and Application
It is important to check whether the nitrogen in operation is in an isothermal state or adiabatic state.
If compression (or expansion) is slow, (more than 3 minutes) so that the gas maintains approximately constant temperature, the condition is isothermal.(For example, pressure stabilization, volume compensation, counter balancing, lubrication circuits). In other cases (energy accumulator, pulsation damper, shock wave damper, etc.) owing to high speed transfer heat inter-change is negligible, and therefore the condition is ADIABATIC. As a guide the adiabatic condition will exist when the compression or expansion period is less than 3 minutes.
4). Operating temperature
Operating temperature will determine the choice of materials for the bladder and steel shell and will also have an influence on the pre-loading pressure, and consequently the accumulator volume.
5). liquid chemical types
This will determine the choice of material.
6). Maximum required flow rate
The volume Vc and/or the size of the connection is influenced by the speed of response.
7). Location
It is important to know the eventual destination of the accumulator in order that the design can meet local design and test parameters.
Based on the foregoing it is possible to choose a suitable accumulator for the specific application required.
2. Nitrogen gas pre-charging pressure
The accurate choice of pre-charge pressure is fundamental in obtaining the optimum efficiency and maximum life from the accumulator and its components. The maximum storage (or release) of liquid is obtained theoretically when the gas pre-charge pressure P0 is as close possible to the minimum working pressure.
For practical purposes to give a safety margin, and to avoid valve shut-off during operation, the value (Unless otherwise stated) is: Po=0.9P1
The limit values of P0 are:Po min≥0.25×P2,Po max≤0.9P1
Special value are used for:
1). Pulsation damper and shock absorber
Po=0.6-0.75Pm or Po=0.8P1 where: Pm= average working pressure.
2). Hydraulic line shock damper
Po=0.6-0.9Pm where: Pm=average working pressure with free flow.
3). Accumulator + additional gas bottles
Po=0.95-0.97P1 Value P0 is valid for maximum operating temperature required by the user.
Checking or pre-loading of accumulator takes place generally at a different temperature to the operational one θ2, so that the value P0 at the checking temperature θc, becomes:
Poc=po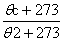
forθc=20℃ we have:Po(20℃)=Po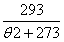
Note: Pre-charge pressure of accumulator directly supplied from the factory at a temperature of 20℃.
3. Calculation principles
Compression and expansion of gas inside the accumulator takes place according to the Boyle-Mariotte law regarding the status change in the perfect gases:
Po×Von=P1×V1n= P2×V2n
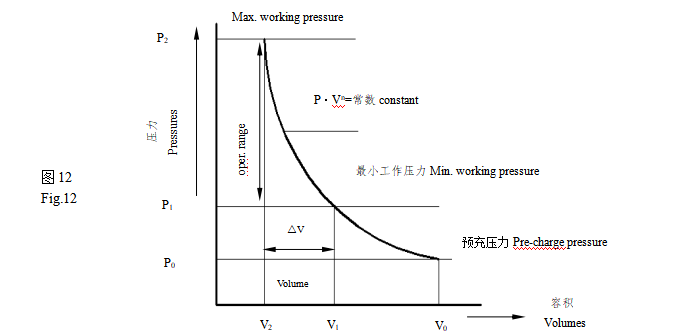
The PV diagram Fig.12 shows the “pressure-volume” relation-ship for the accumulator.
It is the maximum volume of gas which can be stored in the maximum volume of gas which can be stored in the accumulator and it is equal to, or slightly lower than, nominal capacity.
V1=nitrogen volume at pressure P1(liters)
V2=nitrogen volume at pressure P2(liters)
V=Volume of discharged or stored liquid(liters)
Po=pre-charge pressure(bar)
P1=pre-charge pressure(bar)
Po=pre-charge pressure(bar)
n =Polytropic exponent
The curve of volume variation as a function of pressure is dependant on the exponent n, which for nitrogen is contained between the limit values of:
n=1 In case compression or expansion of nitrogen takes place so slowly that a complete interchange of heat is allowed between gas and environment, that is at constant temperature; the condition is isothermal.
n=1.4 When operation is so quick that no interchange, of heat can take place, the condition is adiabatic.
These are theoretical and not practical conditions.
It is however possible to state, with reasonable accuracy that when an accumulator is used as a volume compensator, leakage compensator or as a lubrication compensator and pressure compensator, the condition is isothermal. In the remaining applications, such as energy accumulator, pulsation damper, emergency power source, dynamic pressure compensator, water hammer absorber, shock absorber, hydraulic spring, etc., it is possible to state, with reasonable accuracy that the condition is adiabatic.
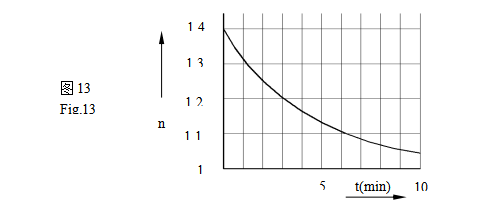
Should a more accurate calculation be needed, it is possible to use intermediate values of n as function of t. that is of expansion or compression time, according to diagram fig.13.
NOTE: In all calculations pressures are expressed as absolute bar and temperatures as Kelvin degrees.
4. Volume calculation
n = 1,Boyle-Mariott
When n=1 the boyle-Mariotte law becomes:
Po×Vo=P1×V1= P2×V2
so that V1= Vo×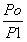
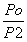
The difference between volume V1 (at minimum operation pressure) and V2 (at maximum operating pressure) gives the amount of stored liquid (see Section 1.1)
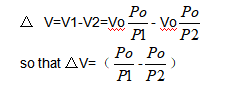
Accumulator volume will be 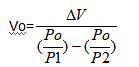
which could be also written: 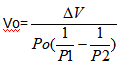
Which shows that accumulator volume increases when △V is increasing, when Po is decreasing and when the difference between the two operation pressures P1 and P2 is decreasing.
5. Volume compensator
A typical example of calculation in the isothermal condition is when the accumulator is used as a volume compensator.
△V= Vt×(θ2-θ1)-(ß×3α)
where:
Vt=piping volume(升Liters)
θ2 =max. temperature(℃)
θ1= min. temperature(℃)
ß = cubic expansion coefficient of fluid(1/℃)
α = linear expansion coefficient of piping(1/℃)
P1= min, permissible operating pressure(巴bar)
P2= max. permissible operating pressure(巴bar)
necessary volume will be:
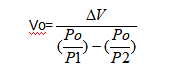
6. Leakage compensator
Accumulator volume be:
ΔV=Q1×t
Po=0.9×P1
P1=min, permissible operating pressure(bar)
P2=max. permissible operating pressure(bar)
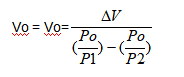
7. Volume calculation
Staring from the basic formula
Po×Von=P1×V1n= P2×V2n
And following what is shown for isothermical calculation, we have:
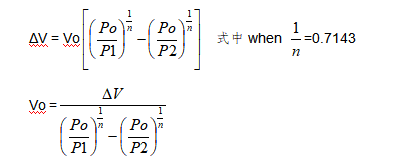
Formulas are valid when operation is taking place in adiabatic conditions both in the expansion as well as in the compression phase.
Bear in mind however that accumulator yield, and therefore the accumulator calculation is influenced by both operating temperature and pressure.
8. Emergency energy reserve
Typical occasion when storage is slow (isothermal) and discharge is quick (adiabatic).
Volume will be given by:
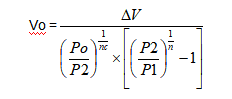
and stored volume by:
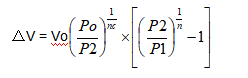
n =1.4 adiabatic coefficient(quick discharge phase)
nc = 1-1.4polytropic coefficient(slow storage phase)
Value is a function of time and it will be derived from the diagram in Fig.13.
In the majority of cases it is possible to suppose nc=1, so that calculation is simplified and result is not affected:
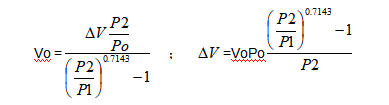
9. Pulsation compensator
A typical calculation in adiabatic conditions due to high speed storage and discharge.
The liquid amount △V to be considered in the calculation is a function of type and capacity of pump.
△V=k×q
Volume becomes:
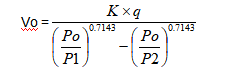
q=Pump displacement(liters)
=A×C(piston surface×stroke)=Q/N(flow rate/strokes)
P=average working pressure(bar)
P1=P-X(bar) P2=P+X(bar)
α =remaining pulsation±(%)
K=Coefficient taking into account the number of piston and if pump is single or double acting.
Pump type K
1 piston, single acting 0.69;
1 piston, double acting 0.29;
2 pistons, single acting 0.29;
2 pistons, double acting 0.17;
3 pistons, single acting 0.12;
3 pistons, double acting 0.07;
4 pistons, single acting 0.13;
4 pistons, double acting 0.07;
5 pistons, single acting 0.07;
5 pistons, double acting 0.023;
6 pistons, single acting 0.07;
7 pistons, double acting 0.023;
10. Hydraulic line shock suppression
A rapid increase in pressure caused by a high acceleration or deceleration in flow is commonly known as water hammer. The extent of over pressure , ΔPmax, that takes place in piping when a valve is closed is influenced by the length of the piping, the flow rate, the density of the liquid and the valve shut down time.
ΔPmax=2γLv/(t×105)
The volume of the accumulator required to reduce shock pressure within predetermined limits ΔP, is obtained with:
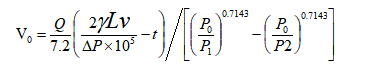
Where: V0=accumulator gas capacity (litres)
Q=flow rate in the piping (m3/h)
=specific gravity of liquid (kg/m3)
L=total length of piping (m)
V=flow velocity (m/s)= 103Q/3.6S
S=internal pipe section (m m2)=πd2/4
d=internal pipe diameter(mm)
ΔP=allowable over pressure(bar)
P1=operating pressure by free flow (absolute bar)
P2 =max. allowable pressure (absolute bar)= P1+ΔP
t=deceleration time (s) (valve shut down, etc.)


